Девета лекция

Щутгарт, 9 януари 1921 година

Стигнахме до момента в нашето разглеждане, от който трябва да се придвижваме нататък крайно внимателно, за да виждаме ясно, доколко опасно е да излезем от реалността с нашите представи и оставаме ли вътре в границите на реалните представи, тоест дали сме избегнали опасността.

Сега ще стане дума за това, че последния път предложих да се сравнят два факта: появата на кометните феномени вътре в планетната система (в края на краищата, разбира се, вътре в планетната система, макар тя и да не се намира с тях в същата връзка) и това, което наблюдаваме при оплождането. Но за да се стигне изобщо до представи, които биха били донякъде обосновани, е нужно на първо място да се види – възможно ли е все пак да се изнамерят отношения между две неща, които във външния свят на фактите изглеждат толкова отдалечени едно от друго. Методологически няма да постигнем целта, ако не успеем да посочим нещо, където се намира нещо подобно, което може да ни придвижи по-нататък в нашите разглеждания.

Видяхме, как от една страна трябва да използваме елементите на фигурите и формално математическото, и как, обаче, отново биваме подтиквани по някакъв начин да постигаме качественото, някак да се приближаваме към качественото. Затова нека днес добавим нещо, проявяващо се по отношение на човека при разглеждането на този човек, който в крайна сметка е отражение (както можем да видим това от отделните неща в тези лекции), отразява небесните явления по някакъв начин, който тепърва трябва да установим. Доколкото човек е такъв, трябва по някакъв начин да постигнем яснота по отношение на самия човек. Трябва в известно отношение да разберем образа, от който искаме да изходим, трябва да разберем вътрешната перспектива. Както за изобразения образ първо трябва да си изясним, какво означава определен ракурс или нещо подобно, за да преминем от този образ към съотношенията на пространството, тоест да съотнесем образа с неговата реалност, така, ако искаме да интерпретираме от човека, трябва детайлно да се спрем на реалностите във вселената, първо да стигнем до яснота по отношение на човека. Но е изключително трудно, самите ние бидейки хора, да се приближим до човека с някакви постижими представи. Затова днес искам, изхождайки от прости отношения, да изведа пред душите ви, бих казал, постижимо-непостижими представи, представи, които вероятно отдавна са известни на мнозина от вас, но които все пак трябва да ги прекараме в определена връзка пред нашите души, за да се ориентираме изобщо по отношение на обхващането с представи на външния свят на основата на тези представи, които отчасти изглеждат доста лесно постижими, но отчасти, в определени граници, отново се оказват съвсем непостижими.

Може да ви се стори като принуда, че отново и отново подчертавам, че за разбирането на небесните явления трябва да се върнем към представния живот на човека. Все пак е ясно, че колкото и внимателно да описваме небесните явления, в тях няма да имаме нищо друго, освен някакъв вид оптичен образ, пронизан от всевъзможни математически представи. Именно това, което ни дава астрономията, има основната характеристика да бъде чист образ. Затова, ако искаме да се справим, трябва детайлно да се спрем на възникването на образа в човека, иначе няма да можем да заемем правилна позиция по отношение на това, което може да ни каже астрономията. И тук бих искал да взема днес за изходна точка нещо съвсем просто в математиката, за да ви покажа, как в една друга област, освен тази, в която ни доведоха относителните величини на периодите на въртене на планетите, вътре в самата математика се появява елементът на непостижимото. Това го срещаме, когато обичайните криви ги разглеждаме в определена връзка[1]. Мнозина от вас вече познават тези неща и аз бих искал днес само да им хвърля светлина от една по-особена гледна точка.

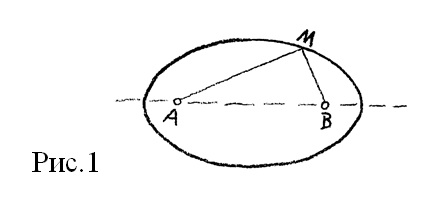
Ако разглеждаме известната ви елипса с два фокуса А и В, то, както знаете, елипсата се характеризира с това, че за коя да е точка М от елипсата е валидно, че сбора на разстоянията а + в от двата ѝ фокуса остава постоянен. Елипсата се характеризира с това, че сборът от разстоянията на коя да е точка до двете фиксирани точки, до двата фокуса, остава постоянен (рис. 1).

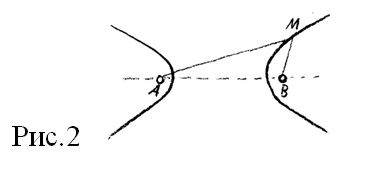
Освен това, имаме втора крива, хипербола (рис. 2). Знаете, че тя има два клона. Тя се характеризира с това, че разликата от разстоянията на коя да е нейна точка до двата фокуса a - b е постоянна величина. И така, в елипсата имаме крива с постоянен сбор, а в хиперболата крива с постоянна разлика. Тогава можем да се запитаме: как би изглеждала крива с постоянно произведение?

Често съм ви обръщал внимание върху тази крива с постоянно произведение – така наречената крива на Касини[2] (рис. 3). Да разгледаме предмета по следния начин: тук имаме две точки А и В и разглеждаме точка М и нейните разстояния до А и В. И така, имаме едно разстояние АМ и друго разстояние ВМ и поставяме изискването тези две разстояния, когато ги умножим, да са постоянна величина.

Тази постоянна величина за опростяване на пресмятанията ще обознача с b², а разстоянието АВ ще обознача с 2а . Ако приемем средата между А и В за начало на координатна система (О) и за всяка точка, удовлетворяваща това условие, изчислим ординатата – тоест ако позволим тук на точката да обиколи, така че за всяка точка от тази крива винаги да важи АМ х ВМ = b² , то за ординатата на коя да е точка, която ще наречем у, ще получим следното уравнение – ще ви съобщя само резултата по простата причина, че всеки може лесно да направи това изчисление. То може да се намери във всеки съответен учебник. За у получаваме следното значение: 

Ако тук (пред вътрешния корен) отчетем, че не можем да използваме отрицателен знак преди всичко защото в този случай ще получим мнимо значение за у, значи можем да вземем предвид само положителния знак и ще получим:

Ако сега прекараме съответната крива, ще получим елипсоподобна, но несъвпадаща с елипса линия, която по името на откривателя си е наречена крива на Касини. Наляво и надясно тя е симетрична относно оста на ординатата, а нагоре и надолу е симетрична относно оста на абсцисата. Това е, което следва да се установи.

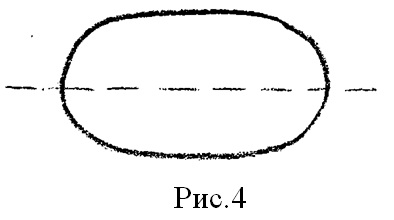
Но тази крива получава различни форми, и това е, което е важното в нея за нас. Тази крива приема различни форми в зависимост от това дали b, както съм го взел тук, е по-голямо от а, равно на а, или по-малко от а. Начертаната току що крива възниква, когато b > а , и, освен това, трябва да бъде изпълнено определено условие, тоест b да бъде по-голямо или равно на . А именно, ако , то тук горе и долу имаме отчетлива кривина. Ако , тук в тази точка горе и долу кривата преминава в права, кривата става толкова плоска, че горе и долу тя почти се превръща в права (рис. 4).

Но ако стигнем до там, че , тогава се изменя цялото очертание на кривата. Тя получава такава форма (рис. 5). А при b=a кривата придобива съвсем особена форма (рис. 6). Тя по определен начин се придвижва назад в себе си, пресича себе си и се оказва от другата страна, и получаваме специалната форма на лемнискатата, така че лемнискатата представлява особена форма на кривата на Касини.

Особената форма е обусловена от отношението на постоянните величини, срещащи се в уравнението на кривата, в характеристиката на кривата. В уравнението имаме само две такива константи b и a, и от отношенията на тези постоянни величини зависи формата на кривата.

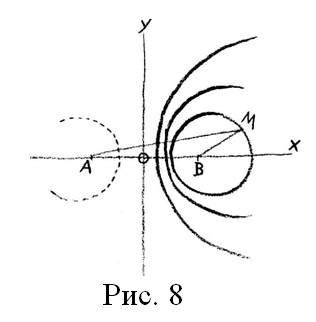
Но е възможен и трети случай, когато b

Защото в смисъла на математическото ѝ уравнение това не са две криви, а една крива, също както тази или тази, или тази (рис. 3-5). Ето при тази крива (лемнискатата) работата е в прехода. Тук точката, описваща кривата, извършва този път, върви надолу, тук пресича своя предишен път и се оказва от другата страна. Тук (рис. 7) трябва да си представяме следното: когато точка M се движи по тази линия, тя вече не пресича просто тук пътя от другата страна, тя не прави това, а пресича пътя точно както тук (на лемнискатата) описва крива и след това отново стига до това, да се окаже тук. И така, виждаме, че това, което носи точката по линията, изчезва тук в средата. Ако искате да разберете кривата, можете само да си представите, че те изчезва в средата. Какво трябва да направите, ако се опитвате да създадете непрекъсната мисловна картина за тази крива? Ако си представяте такава крива (първите три вида) – казвам това между другото, за обикновения гражданин, – то това е лесно да се направи. Можете непрекъснато да си представяте една точка и няма да стигнете дотам, представата ви да се прекъсне. Тук (на лемнискатата), обаче, трябва вече да модифицирате този удобен начин за просто преминаване в кръг. Но тук все още това е възможно. Можете да удържите представата. Но по-нататък, когато стигнете до тази крива (вида с два клона), която вече не е някаква обикновена крива, ако искате да си я представите, за да останете в рамките на непрекъснатата представа, трябва да си кажете: пространството вече не ми дава за това никакво основание. Придвижвайки се тук (от 1 до 2) с моята представа[3], ако не искам да прекъсна тази представа и да разглеждам другия клон отделен сам по себе си, трябва да изляза с представата си от пространството (от 3 до 4) – аз не мога да остана вътре в пространството. Виждате, че самата математика ни предоставя факти, които ни заставят да излезем от пространството, ако искаме да останем в рамките на непрекъснатата представа. Действителността е такава, че тя изисква от нас да излезем с представите си от пространството. Тоест, в самата математика срещаме нещо, показващо ни в определена степен, че трябва да оставим пространството ако чисто и просто искаме да се справим с тези представи. В това, което сами предизвикахме със своите представи, когато започнахме да мислим, трябва да мислим по-нататък по такъв начин, че пространството вече с нищо не ни помага. В противен случай не биха били взети предвид всички възможности в уравнението.

Нееднократно се сблъскваме с такива неща, когато преживяваме подобна представа. Искам само да ви обърна внимание какво следва, когато продължим в тази посока. И така, елипсата е геометрично място от точки и се характеризира с това, че е линия на постоянния сбор. Хиперболата е кривата на постоянната разлика. Кривата на Касини (касиноидата) с нейните различни форми е линията на постоянното произведение. Също така, когато тук имаме А, тук В и тук точка М и образуваме частно от делението на ВМ на АМ, може да се намери линия на постоянното частно. И така, трябва да намерим различни точки, М1, М2 и така нататък, за които отношенията

и така нататък са винаги равни едно на друго и са винаги равни на определена постоянна величина. Обаче тази крива е окръжност. Когато търсим точки М1, М2, получаваме окръжност, която се намира примерно в такова отношение към точки А и В (рис. 8). Така че можем да кажем: наред с тривиалното определение за окръжност, а именно, че окръжността е геометрично място от всички точки, равноотдалечени от една постоянна точка, съществува друго определение за окръжност: окръжност е такава линия, за всички точки от която е изпълнено следното условие – частните от разстоянията им от две постоянни, неподвижни точки, са равни.

И така, тук за окръжността имаме възможност да погледнем и към нещо друго. Защото, виждате ли, ако изразим ВМ : АМ чрез m : n , тоест

винаги ще получим съответстващите данни в уравнението. По такъв начин можем да намерим окръжността. Ако се направи това, ще се получат различни форми на окръжности, в зависимост от отношенията на m към n: ако n е значително по-голямо от m, ще получим силно огъната окръжност, когато n става по-малко, ще получим по-малко огъната окръжност (рис. 8 вдясно). И така, окръжността става толкова по-голяма, колкото по-малко m се различава от n. Проследявайки по-нататък това отношение m : n, виждаме, че окръжността постепенно преминава в права. Можете да проследите това в уравненията. Тя се превръща в самата ординатна ос[4]. Окръжността се превръща в ординатна ос при m=n, тоест когато m:n = 1. По такъв начин окръжността постепенно се превръща в ординатна ос, в права.

Не трябва много да ви учудва, че това става. Това е нещо, което можем да си представим. По различен начин ще стои работата, ако поискаме да отидем по-нататък и си кажем, че окръжността става все по-плоска и по определен начин, благодарение на вътрешното сплескване, възниква правата. Това става просто защото се изменя постоянното отношение в даденото уравнение. Естествено, това постоянно отношение даже може да надхвърли 1, така че тук се появяват дъги на окръжности (вляво от оста у), но какво да правим тогава с нашите представи? Необходимо е нещо съвсем особено. Тогава трябва да си представим именно окръжност, която не е огъната навътре, а навън. Естествено, няма да успея да ви изобразя тази окръжност[5], но е възможна окръжност, която е огъната навън.

При обикновената окръжност имаме кривина, обърната навътре, нали така? (окръжност a рис. 9, защрихованата страна). Ако проследим пътя ѝ, тя ще се затвори. Ако приемем съответстващото значение за константата, която имаме в уравнението, ще получим права. Тук тя има своята кривина от другата страна (вдясно от правата, защрихованата страна). Но тази кривина не ни е толкова удобна, както другата кривина. Другата кривина винаги има тенденция към центъра на окръжността. Тази кривина (при правата) ни показва, че централната точка, както се казва, е безкрайно отдалечена някъде. Но сега тук (вляво от правата) в нас възниква мисълта за окръжност, която е изкривена навън. Нейната кривина в такъв случай не се намира тук (окръжност b, незащрихованата страна), иначе това би била обичайната тривиална окръжност, а нейната кривина се намира тук (окръжност b, защрихованата страна). И именно затова вътрешна страна на окръжността тук не е тази (незащрихованата страна), а външната страна на окръжността, и ето тази (защрихованата) е вътрешната страна на окръжността.

Сега ви моля да сравните с това, казаното от мен тук: кривата на Касини с нейните разновидности – с лемнискатата и с формата, където тя има два клона. Тук изобразихме окръжността така, че един път тя има такава (обичайна) кривина, тук това е нейната вътрешна страна, а това нейната външна страна. Имаме втора форма на окръжността (b) – сега можем само да маркираме окръжността, – където кривината се намира тук (отвън), тук се намира вътрешността ѝ (защрихованото), а тук външната страна (незащрихованото). Ако сравним първата форма на окръжността с кривите на Касини, би съответствала примерно на тяхната затворена форма, чак до лемнискатата. А сега имаме втора окръжност (b), която трябва да бъде представена в това направление (навън), която има кривина тук: нейната вътрешна част се намира тук, а външната – тук. Виждате: реалността е такава, че ако имаме работа с произведение, получаваме формата на кривата на Касини, при която, когато бъдем изхвърлени от пространството, отново можем да начертаем на другата страна втори клон. Тогава тя отново стои в пространство. Но за прехода от единия клон към другия биваме изхвърлени от пространството. Тук, в окръжността, нещата вече се усложняват. Тук съвсем определено при прехода от окръжността към правата сме изхвърлени от пространството, но в този случай вече изобщо не можем да рисуваме нещо затворено. Ние не стигаме до това. В мислите си все още можем да намекваме пряко на пространственото, когато преминаваме от кривата на постоянното произведение към кривата на постоянното частно.

Изключително важно е човек да се отдава на създаване на представи, които, бих казал, все още се промъкват в такива криви. Уверен съм, че много хора занимаващи се с математика, макар и да стигат до такива прекъсвания, след това, по същество, си създават малко по-удобна представа, доколкото те се придържат само към това, което е зададено с формулите, но не преминават към нещо, което трябва да съпровожда формулите като действителна, непрекъсната представа. Още нито един път не съм виждал, в излагането на учебния математически материал високо да се цени формирането на такива представи. Може би, не съм съвсем в час и искам да попитам присъстващите тук математици г-н Блюмел и г-н Баравал[6], това така ли е – може би днес някъде в университетите придават на това голямо значение? (Г-н д-р Карл Унгер[7] обръща внимание на използването на кино). Да, това е псевдоформа, когато това искат да го представят вътре в емпиричното пространство, тоест посредством такъв киноапарат или нещо подобно. Тук винаги има някаква измама. Невъзможно е да се представи това по съответстващ начин в емпиричното пространство, ако не се прибегне към измама.

Сега става дума за това, има ли някъде в действителността нещо, реално стимулиращо ни да мислим в такива криви. Това е, което бих искал да поставя като въпрос. Но преди да премина към характеристика на това, което примерно би могло да съответства на това в действителността, бих искал да добавя нещо, което, може би, ще облекчи прехода ви от тези абстрактни представи към действителността. Ето за какво ще стане дума. В теоретичната астрономия, в теоретичната физика може да се постави и друг проблем. А именно, може да се постави такъв проблем: да допуснем, че тук в точка А се намира източник на светлина, и този източник на светлина осветява точка М (рис. 10). Точката М се наблюдава от точка В по отношение на интензивността на осветеността ѝ. Тоест от точка В посредством някакви оптични инструменти се наблюдава осветеността на точка М от източника на светлина А. От самосебе си се разбира, че ще видим по различен начин степента на осветеност в зависимост от отдалечеността на В от точка М. Но съществува траектория, която може да опише тази точка М, движейки се така, че, бидейки осветена от А, за В тя винаги сияе с една и съща сила на блясъка. Има такава траектория. И така, можем да попитаме: каква трябва да бъде траекторията на точка М, която се осветява от неподвижната точка А, така че за другата неподвижна точка В, нейната осветеност винаги да има еднаква интензивност[8]?

Тази крива, по която се движи такава точка, е крива на Касини! Оттук виждате, че тук в пространствено отношение, в сложната крива се влага нещо, преминаващо вече в качествено. Качеството, което вече виждаме в светлинното сияние, в интензивността на сиянието, това качество зависи тук от елемента на формата в пространствените отношения.

Исках да ви приведа този пример само за да видите някакъв път, който превежда от това, което може да се разбира фигурално-геометрически, към качественото. Но, от друга страна, този път в известно отношение все пак е дълъг. И сега ще преминем към нещо, за което, разбира се, биха били нужни месеци, за да се представи то във всички подробности, и въпреки това, бих искал да ви насоча към него. Непременно трябва да отчетете, че искам само да ви дам насока, чиято по-нататъшна разработка, а именно по-нататъшната разработка по отношение на детайлите, които, проверявайки ги винаги ще ги намерите, предоставям на вас. Защото, виждате ли, между духовната наука и днешната емпирична наука трябва да се завържат отношения, предоставящи много широко поле за действие, извънредно широко поле за действие. Ако са дадени ръководните насоки, тази работа може по определен начин да се осъществи. Това е възможно. Нужно е само по определен начин да се проникне в емпиричните явления.

Сега, обхващайки проблема от съвсем друга страна, – опитахме се тук да го обхванем до известна степени от математическата страна, – този, който се занимава с човешката организация, не може да избегне нещо, което нееднократно вече се е отбелязвало в нашия кръг и особено в много отношения се е подчертавало по време на обсъжданията, с които завърши дорнахския курс за лекари през пролетта на 1920 г.[9]. Той не може да избегне това, че главовата организация се намира в определени отношения с останалата организация на човека, например с организацията на обмяната на веществата. Съществува, преди всичко, неопределима връзка между това, което става в третата човешка система, в системата на обмяна на веществата с нейните органи, и това, което се разиграва в главата на човека. Обаче това съществуващо тук отношение е много трудно разбираемо. Колкото и ясно тези отношения да са представени в явленията, колкото и ясно да е видно, например, че с определени заболявания са свързани деформации на черепа, главата и други подобни неща, колкото и ясно да се проследяват тези неща за този, който ги проследява разумно биологично, все пак е трудно да се формират разбираеми представи. Хората обикновено се спират дотам, че да кажат: трябва да се намери някаква връзка между това, което се разиграва в главата, и това, което се разиграва в останалия организъм на човека. – Тази представа затова е толкова трудно осъществима, защото именно преходът от количественото към качественото се удава на човека толкова трудно. Ако не се учим да търсим този преход посредством духовнонаучната методология и, съвсем независимо от това, което предлага външния опит, все пак по определен начин да разпространяваме такъв род представи, който се използват за количественото и върху качественото, ако не се възпитаваме за това методологично, за нашето разбиране винаги ще се изправя привидната граница на външните явления.

Бих искал също да ви покажа, как можете методологично да възпитате себе си да мислите качествено, подобно на количественото мислене. На всички ви е познато явлението на слънчевия спектър, обикновения непрекъснат спектър. Знаете, че тук обикновено преминаваме от червения към виолетовия цвят. Знаете също, че Гьоте е полагал усилия да покаже, че този спектър в определен смисъл е обратен спектър на това, което ще се получи, ако с помощта на призма по определен начин се отнесем с тъмнината така, както обикновено се отнасяме със светлината. Както е установил Гьоте, тогава получаваме определен вид обратен спектър[10].

При обикновения спектър имаме зелен цвят преминаващ тук във виолетов, а на другата страна – преминаващ в червен (рис. 11), нали така? А в спектъра, който е получил Гьоте когато е наложил черна лента, той е получил тук прасковен, и на едната страна отново червен, а на другата страна – виолетов (рис. 12). По определен начин имаме две цветови ленти, които в центъра са противоположни една на друга, качествено противоположни, и двете за нас преди всичко бягат, бих казал, в безкрайността. В началото може просто да си представим, че тези оси, продължаващите оси на обикновения спектър не са проста права, а окръжност, както и всяка права е окръжност. Ако тази права е окръжност, тя самата се връща в себе си, и тогава можем просто тази точка тук, където се появява прасковеното, да я разглеждаме като друга точка, в която се срещат виолетовото, отиващо надясно, и червеното, отиващо наляво. Лявото и дясното се срещат, разбира се, в безкрайната далечина. Но ако ни се удадеше – не знам известно ли ви е, че за изследванията в това направление трябваше да създадем една от първите експериментални установки в нашия научно-физически институт[11] – по определен начин да затворим спектъра в самия себе си, тогава и тези, които в началото не искаха да разбират тези неща, обмисляйки това, биха видели, как в действителност и тук имаме работа с качественото. Такива представи по същество са крайни математически представи, когато сме принудени, както в синтетичната геометрия, вътрешно напълно обективно да разглеждаме правата също и като кръг, когато сме принудени да допускаме за правата линия като безкрайно отдалечена точка само една точка, когато сме принудени като граница на равнината отгоре и отдолу да допускаме не някаква линия, а като граница на равнината да допускаме една единствена права линия; когато сме принудени да си представяме границата на безкрайното пространство не като сфера или нещо подобно, а като равнина. Но ако искаме да разглеждаме само сетивно-емпиричната действителност, такива представи също определено се превръщат в гранични представи на сетивно-емпиричната действителност.

И така, това ни довежда до нещо, което в противен случай винаги ще си остане неизвестно. Вече говорих за това. Това ни довежда до мислене с представи, които можем да придобием, когато привеждаме кривата на Касини във форма на лемниската към форма с два клона, тази форма с два клона, където трябва да излезем от пространството и после да сравним това с представеното ни в емпиричната действителност. Правите същото това, когато прилагате математиката към емпиричната действителност. Това, което е представено в триъгълника го наричате триъгълник, доколкото триъгълникът първо е конструиран математически. Конструктивно формираното вътре във вас го прилагате към външните форми. Процесът, за който сега говорих, е същият процес, само че по-сложен, когато мислите като една крива с два клона двуклонната крива на Касини. Ако приложите тази представа към това, което в главата на човека съответства на нещата в останалия организъм, трябва да мислите така, че тук в главата съществува зависимост от останалия организъм, която може да се изрази посредством такава връзка, посредством това уравнение (с. 68), което обаче предизвиква прекъсната крива. Не можете да проследите това с помощта на анатомичния метод. Ако искате да проследите проявяващото се в главата във връзка с проявяващото се в метаболизма, трябва да излезете от това, което тялото физически съдържа в себе си. И така, трябва да проследявате човешкия организъм с помощта на представите, които е невъзможно да се получат, ако за всеки отделен член на тези представи искаш да имаш адекватна сетивно-емпирична представа. Трябва да се излезе от сетивно-емпиричното към нещо друго, ако някой иска да разбере, каква е тази връзка в човека.

Ако сега това методологически се проследи по-нататък, ако действително се пристъпи към такова разглеждане, става нещо извънредно съдържателно. Защото човешкият организъм наистина е включен в нещо, което не може да се обхване само анатомично. И както при кривата на Касини биваме изгонени от пространството, по същия начин при разглеждането на човека, чрез самия способ на разглеждане, сме изгонени от тялото. Преди всичко трябва да се схване чрез представите, че за цялостното разглеждане на човека биваш изхвърлен от това, което в човека трябва да се разбира с физическо-емпиричния метод. Изтъквайки такива неща, абсолютно не се греши по какъвто и да начин по отношение на научността. Те са извънредно далеч от това, което често хипотетично се представя като чисти фантазии по отношение на природните явления. Защото тези неща действително връщат към начина, по който човек стои вътре в света. Вие не търсите по нещо, което обикновено не съществува, а търсите съдейки по това, което съществува абсолютно по същия начин, както и това, което се изразява във връзката на математизиращия човек с емпиричната действителност.

Въпросът съвсем не е в това да се занимаваме с търсене на някакви необосновани хипотези, а в това, доколкото действителността очевидно е сложна, да се търсят във вътрешната действителност и други познавателни отношения, освен простото съществуващо отношение на математизиращия човек към физически-емпиричната действителност. Ако веднъж сте обърнали внимание на такива неща, това ще ви стимулира да изследвате също, например, ставащото извън човека в другите области, освен областта на астрономията, ставащото извън човека, например в тези явления, които наричаме физически, химически, и това после ще ви стимулира да търсите отговор на въпроса, дали в живота на човека явленията, които във външния свят разглеждаме като химически, протичат по същия начин, или тук те също се нуждаят от преход, който по определен начин извежда от пространството.

Помислете сега за важния въпрос, който следва от това. Тук става някакво химическо явление, тук е границата с вътрешния човек (рис. 13).

Ако това химическо явление предизвикваше друго така, че човек би реагирал тук (вътре), от самосебе си се разбира, че ако оставахме в емпиричното поле, посредник би било пространството. Но ако това явление продължава в човека, е възможно, благодарение на това, че той употребява хранителни продукти и процесите продължават вътре в него, да възникне въпросът: остава ли в същото пространство, в което е станало отвън това, което действа тук по силата на химическия процес, когато то продължава в човека? Или, може би, трябва да излезем от пространството? Тук имаме аналогия с окръжността, която преминава в права линия. И когато търсите другата ѝ форма, където това, което обикновено е обърнато навън, е обърнато навътре, тогава тук вие изцяло се намирате извън пространството.

Възниква въпросът, не се ли нуждаем от такива представи, които изцяло ни извеждат от пространството, ако трябва да останат непрекъснати, ако това, което става във външния свят, извън човека, го проследяваме по-нататък в неговото течение, когато то продължава вътре в човека. Единственото, което може да се каже против такива неща, е че те предявяват към способностите на човека по-високи изисквания от тези, с които днес се подхожда към явленията, и затова те са неприятни даже при преподаването в университетите. Те са доста неприятни, защото тук, собствено, се изисква, преди човек да подходи към дадени явления, да е усвоил нещо, което ще му позволи да разбира тези явления. Днес в нашето преподаване изобщо не съществува нищо подобно, но това трябва да го има, това безусловно трябва да го има, иначе, говорейки за явленията, без да сме надникнали някак си в реалността, просто ще се окажем в нещо абсолютно несъответстващо. Защото представете си например, какво би станало, ако някой наблюдава окръжност, как тя се огъва на тази страна (рис. 9 a), а тук съзерцава това огънато на тази страна (b), но той си остава филистер и съвсем не схваща, че сега окръжността се огъва на другата страна. Той казва: това не може да го бъде, окръжността да се огъва по такъв начин, аз трябва да преместя кривината тук (окръжност c вместо b), аз просто трябва да съм от другата страна. Изглежда, че в случая той говори за едно и също, но той променя своята позиция.

Именно така просто днес се правят нещата, когато се описва вътрешно човекът в сравнение с това, как се описва външната природа. Казва се: това, което се намира вътре в човека, изобщо не съществува, но аз поставям себе си в човека и казвам, че кривината е обърната насам (c). Тоест аз разглеждам вътрешно без да отчета, че кривината се е обърнала към мен. Превръщам това, което се намира вътре в човека, във външна природа. Аз просто продължавам през кожата външната природа. Аз се обръщам, тъй като не искам да се съглася с другата форма на кривината, и след това теоретизирам. Всъщност това, което се излага в днешно време е трик, и единствената цел на този трик е да удържа удобните представи. Хората не искат да се сблъскат с действителността и да имат работа с нея, а просто се обръщат и вместо да разглеждат човека – това е просто за сравнение – отпред, го разглеждат отзад и стигат до различните теории за човека.

Ще продължим да говорим за това утре.

[1] обичайните криви ги разглеждаме в определена връзка – първото разглеждане на криви от такъв род чрез събиране, изваждане, умножение и деление се намира в трета лекция на GA 286 “Пътища на един нов стил на строителство“. Известно е, че слушателите са били поразени от възможността внезапно да чуят математическа лекция в рамките на художествените лекции, които са били насочени към строителите на Гьотеанума. Едва дълго време след смъртта на Рудолф Щайнер, Карл Кемпер на базата на тази лекция открил, че в основата на хоризонталната проекция на структурата стои кръг с деле­ние в отношение 1:3. С това математическата лекция „ Пътища на един нов стил на строителство“ внезапно намерил своето обяснение. Преди за плановете на зданието са се придържали към други мнения. Лекцията съдържа също подробно представяне на кривата на Касини и нейните форми. Изображението на тази крива в предлагания курс се приближава до даденото в учебника на Любсен (Heinrich Borchert Lubsen, „Ausfuhrliches Lehrbuch der analytischen oder Hoheren Geometrie, zum Selbstunterricht“, II. Auflage 1876). Това и по-ранното издание на книгата ги няма в библиотеката на Рудолф Щайнер. Обаче от GA 28 „Моят жизнен път“ е известно, какво значение са имали математическите книги на Любсен в училищните години на Рудолф Щайнер. Тези ранни издания не съдържат нищо от систематичната мисъл да се свържат кривите с четирите аритметични действия. Областта на делението въобще липсва. Тази системна мисъл изплува едва в новата обработка на съчинението, направена от A. Donadt (15. Auflage, 1908); това издание от 1919 година се намира в библиотеката на Рудолф Щайнер, но забележителното е, че на това място страниците на книгата не са разрязани. Макар да ни се струва очевидно да се съпоставят кривите с четирите аритметични операции, все пак тази мисъл едва ли обичайно се среща в математическата литература. Защото ни­кой не е изявявал желание да свърже кривата на Касини с три други по-прости криви.

[2] крива на Касини – в тази връзка е много интересно, че кривата е възникнала изцяло от астрономическите разсъж­дения, а именно като орбита на Слънцето. Това го е потвърдил синът на Касини (Jacques Cassini „Elements d‘astronomie“, Paris 1740, S. 149-151). При самия Касини (Джовани Доменико Касини, 1625-1712 ), открил кривата, сред неговите многобройни статии няма такава, където да се дава по-подробно разяснение на кривата. Изглежда неизвестно, как той е стигнал до мулти­пликативната крива. По този повод още в 1755 г D‘Alembert (Bd. 5 der Enzyklopadie von Diderot, Artikel „Ellipse, Ellipse de M. Cassini“) е направил само едно пред­положение. Касини, вероятно, се е интересувал из­ключително от елиптичната форма и при публику­ването на своето откритие (на едно от заседанията на Парижката академия) е представил само нея. Другите фор­ми за пръв път били открити от Джеймс Грегори, приятел на Нютон, и били изложени в 1704 г. в докладите на Кембриджското Кралско Общество. Той приключил статията си с изискване изцяло в духа на Нютоновия закон за привличането: „Тази крива трябва да изчез­не от астрономията“. По пътя, който Рудолф Щайнер прокара за разширяване на науката, кривата на Касини доби важно значение. На философския конгрес в Болоня в 1911 г. той я нарече важен пример за медитативно съдържание, посредством което може да се търси разширение на съзнанието към свръхсетивното познание (GA 35 „Философия и антропософия“).

[3] Придвижвайки се тук (от 1 до 2) с моята представа – това в скобите е интерпретацията на издателя на думичката „тук“. На оригиналната картинка няма никакви цифри

[4] Можете да просле­дите това в уравненията. Тя се превръща в самата орди­натна ос – в бележник Nr. 52 (1921) това се проследява по следния начин ( GA 104 „Статии към събраните съчинения на Рудолф Щайнер“): ((x-a)²+y² )½ : ((x+a)²+ y² )½= m : n

(n² – m² )× x² + (n² – m² )× y²-2a(n² + m² )× x+ (n² – m² )× a² = 0. Центърът има координати a× (n² + m² ???? (n² – m² ) , 0

 r = a×2mn : (n²-m² ). m = n Уравнение на ординатната ос. (По технически съображения вместо дробна черта е използван знак за деление, а вместо корен квадратен – ½).

[5] Естествено, няма да успея да ви изобразя тази окръжност – невъзможно е да се изобрази вътрешната ѝ част, доколкото тя се простира до безкрайност; нейният край може да се представи като при обичайния кръг.

[6] Херман фон Баравал – 1898-1973, математик, преподавател по математика и физика, автор на учебници, учител във Валдорфското училище и основател на подобни училища в САЩ

[7] Карл Унгер – 1878-1929, доктор на техническите науки, собственик и ръководител на машиностроителен завод. Работил в областта на теорията на познанието. Член на ръководството на Антропософското общество.

[8] така че за другата неподвижна точка В, нейната осветеност винаги да има еднаква интензивност – във „Hoheren Geometrie [Висша геометрия]“ на Любсен (Lubsen) (виж бел. 74) това свойство на кривата на Касини е дадено в бележките, без подробно обяснение. – Ако точка М отразява по такъв начин изходящата от точка A вълна , както се смята при прилагането на принципа на Хюйгенс (Кристиан Хюйгенс, 1629-1695, холандски механик, физик, астроном и математик), а именно с изотропно и пропорционално падаща интензивност [на светлината], тя действително трябва да описва крива на Касини, така че изходящата от нея вторична вълна да стига до B с постоянна интензивност. При осветяване това важи в случай, че се излъчват изотропно разпространяващи се частици.

[9] дорнахския курс за лекари през пролетта на 1920 г. – GA 201 “Съответствие между макрокосмос и микрокосмос“, особено лекция 2

[10] получаваме определен вид обратен спектър – виж първи и втори естественонаучни курса, GA 320 и 321 “Духовнонаучни импулси за развитие на физиката“, особено лекция 4, съответно 8, 9 и 11. На рис. 12 „син“ и „жълт“ са допълнените външни цветове на обърнатия спектър. Тук става дума само за вътрешната част. Обаче, ако, както в първото издание я приложим отдясно като продължение на рис. 11, така че двата виолетови цвята да са един до друг, ще възникне мислено затворена фи­гура във формата на затваряща се в безкрайността (червеното) права. Тогава жълтото и синьото ще бъдат общи за двата спектъра.

[11] една от първите експериментални установки в на­шия научно-физически институт – по време на втория естественонауче­н курс в Щутгарт е бил основан Изследовател­ският институт. Скоро той е станал жертва на инфлацията от 20-те години. Без оглед на частично положителните първи резултати, експериментите не били завършени. Доста взискателните условия за опитите от 20-те години по-късно не са били реализирани (виж GA 95 „Статии към събраните съчинения на Рудолф Щайнер“).